def L_i(x, y, W):
"""
unvectorized version. Compute the multiclass svm loss for a single example (x,y)
- x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)
with an appended bias dimension in the 3073-rd position (i.e. bias trick)
- y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)
- W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)
"""
delta = 1.0 # see notes about delta later in this section
scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
correct_class_score = scores[y]
D = W.shape[0] # number of classes, e.g. 10
loss_i = 0.0
for j in xrange(D): # iterate over all wrong classes
if j == y:
# skip for the true class to only loop over incorrect classes
continue
# accumulate loss for the i-th example
loss_i += max(0, scores[j] - correct_class_score + delta)
return loss_i
def L_i_vectorized(x, y, W):
"""
A faster half-vectorized implementation. half-vectorized
refers to the fact that for a single example the implementation contains
no for loops, but there is still one loop over the examples (outside this function)
"""
delta = 1.0
scores = W.dot(x)
# compute the margins for all classes in one vector operation
margins = np.maximum(0, scores - scores[y] + delta)
# on y-th position scores[y] - scores[y] canceled and gave delta. We want
# to ignore the y-th position and only consider margin on max wrong class
margins[y] = 0
loss_i = np.sum(margins)
return loss_i
def L(X, y, W):
"""
fully-vectorized implementation :
- X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
- y is array of integers specifying correct class (e.g. 50,000-D array)
- W are weights (e.g. 10 x 3073)
"""
# evaluate loss over all examples in X without using any for loops
# left as exercise to reader in the assignment2018年8月30日 星期四
CS231n: loss function perl
CS231n: Linear classification: Support Vector Machine, Softmax
Two major components
score function:maps the raw data to class scores
loss function:quantifies the agreement between the predicted scores and the ground truth labels.
2.Linear classification(Score Function)
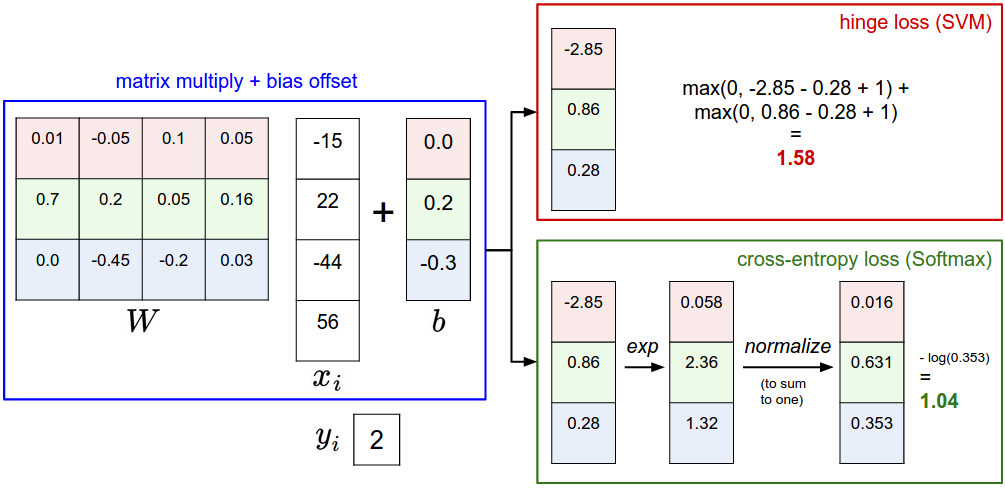
f(xi,W,b)=Wxi+b
SVM : support vector machine(Loss Function)
Li=∑j≠yimax(0,wTjxi−wTyixi+Δ)
threshold at zero max(0,−) function is often called the hinge loss.
Regularization. (用來達成簡單的函數模型而不至於overfitting training data)
R(W)=∑k∑lW2k,l
That is, the full Multiclass SVM loss becomes
L=1N∑iLidata loss+λR(W)regularization loss
or
L=1N∑i∑j≠yi[max(0,f(xi;W)j−f(xi;W)yi+Δ)]+λ∑k∑lW2k,l
Binary Support Vector Machine
Li=Cmax(0,1−yiwTxi)+R(W)
Softmax classifier:(Loss Function)
Li=−log(efyi∑jefj)or equivalentlyLi=−fyi+log∑jefj
H(p,q)=−∑xp(x)logq(x)
score function:maps the raw data to class scores
loss function:quantifies the agreement between the predicted scores and the ground truth labels.
2.Linear classification(Score Function)
f(xi,W,b)=Wxi+b
SVM : support vector machine(Loss Function)
Li=∑j≠yimax(0,wTjxi−wTyixi+Δ)
threshold at zero max(0,−) function is often called the hinge loss.
Regularization. (用來達成簡單的函數模型而不至於overfitting training data)
R(W)=∑k∑lW2k,l
That is, the full Multiclass SVM loss becomes
L=1N∑iLidata loss+λR(W)regularization loss
or
L=1N∑i∑j≠yi[max(0,f(xi;W)j−f(xi;W)yi+Δ)]+λ∑k∑lW2k,l
Binary Support Vector Machine
Li=Cmax(0,1−yiwTxi)+R(W)
Multiclass Support Vector Machine loss
Li=∑j≠yimax(0,wTjxi−wTyixi+Δ)Softmax classifier:(Loss Function)
Li=−log(efyi∑jefj)or equivalentlyLi=−fyi+log∑jefj
H(p,q)=−∑xp(x)logq(x)

訂閱:
意見 (Atom)